The first set had the values 3d, 4d and 6d, Perf.12½.
Steven Roberts also says on How The Companies Worked (about two thirds of the way down)
"The London District Telegraph Company sold its 6d message stamps bound into small books with ten pages of six stamps in 1861."
According to Steve Hiscocks, these were reported to have been issued in booklets of 10 panes of six stamps, but he didn't give any dates.
So far, I have 120 scans of the following:
| 3d Yellow | 4d Blue | 6d Vermilion |
|---|---|---|
| A661, A1112, A1144, A1221, A1262, A1267, A1310, A1320, A1324, A1336, A1338, A1357, A1364, A1379, A1386, A1395(L&H), A1396, A1401, A1404, A1415*, A1423, A1424, A1429, A1443, A1448, A1463, A1469, A1480, A2121, A2382, A4853, A4999. |
A2315, A2333, A2340, A2342, A2354, A2356, A2358, A2364, A2367, A2368, A2375, A2378, A2383, A2392, A2464, A2465, A2466, A2468. |
A1967, A1968, A1979, A1984, A1991, A1993, A2006, A2013, A2017, A2020, A2023, A2032, A2041, A2042, A2057, A2059, A2064, A2065, A2092, A2099, A2102, A2108, A2111, A2114, A2115, A2122, A2130, A2135, A2146, A2166, A2174, A2181, A2193, A2194, A2200, A2210, A2211, A2217, A2226, A2229(L&H), A2338, A2341, A2345, A2371, A2387, A2392, A2414, A2425, A2435, A3543, A3544, A3546, A3547, A3548, A4110, A4418, A4419, A4722, A5304, A5312, A5317, A6244, A6248, A6261, A6269, A6272, A6274, A7404, A7409, A8852, A9855. |
| 32 | 18 | 71 |
* this is apparently a proof. Evidence suggests that these were made some time after production started to test surface coloured rather than coloured paper production.
I have more scans of the 6d than the other two together, so I started with those.
Consecutive serial numbers are usually vertical pairs numbered downwards:



Three digitally reconstructed vertical pairs, the left pair (A1967/A1968 are the lowest numbers I have seen) - courtesy of Steve Lawrie.
The next pair, A2041/A2042 look like they fitted, though with the bottom having additional trimming - courtesy of Steve Lawrie.
The last pair, A2114 of mine and A2115, source unknown, look like they fit.
 |
 |
 |
 A2210 is a good match for A2130, 80 away. A2130 image is courtesy of Corinphila. |
| This pair additionally has A3548 underneath in a horizontal pair with A3543 (see below). - A3546 courtesy of Martien Blank and A3547 courtesy of the late Mike Holt. |
This pair seems to fit. In addition they are the only apparently used ones that I have seen. - A4418 courtesy of Steve Lawrie and A4419 courtesy of Andrew Higson. |
This pair, A2210 and A2211, clearly does not fit, indicating that the stamps are from different vertical columns - both courtesy of Steve Lawrie. |
Horizontal pairs have serial numbers 5 apart, increasing right to left:
 |
 |
| These two look like they were once joined. - A2059 and A2064 Courtesy of Steve Lawrie. | These two also, A1979 Courtesy of Steve Lawrie and A1984 courtesy of Derek Harborne. |
 |
| This 6d pair of stamps indicate that the numbering system is vertical with 5 rows of stamps on the sheet. A3543 and A3548 ourtesy of Andrew Higson. |
 |
| Until recently, these were the highest controls I had seen for the 6d. Again these indicate 5 rows of stamps on the sheet. The selvedge on the right indicates a sheet edge. A7404 and A7409 courtesy of Steve Lawrie. |
Next I need to know how many stamps there were in a sheet.
For low quality work, images could be drawn directly onto a stone with a water-repelling substance.
Flaws could arise at each step of the process :
|
1) Each transfer from the original to a member of the 'Transfer Group' on the transfer stone. These are called primary flaws. 2) Each transfer from the transfer stone to the printing stone. These are called secondary flaws. 3) Each transfer from the printing stone to a sheet of stamps. |
In addition, the printing stone did not last forever. With use, the impressions degraded, altering existing flaws and perhaps adding new ones.
ultimately the surface of the limestone had to be ground down and new impressions laid down from the transfer stone.
Flaws can comprise either marks where they were not intended, of an absence of ink. Sometimes flaws were repaired by 'retouching' by hand.
Distinguishing between these layers of flaws necessarily entails many images and more would be welcome.
Pairs with matching flaws have serial numbers a multiple of 40 apart:

A1991 is mine and A2111 (C2R1) (120 apart) courtesy of Steve Lawrie.


A2114 is mine, A2194 (C2R4) (80 apart) and A6274 (C2R4) (another 4080 apart) courtesy of Steve Lawrie.

A2108 courtesy of Steve Lawrie and A3548 (C3R3) (1440 apart) courtesy of Andrew Higson.



A2064 and A5304 (C4R4) (1760, 1480 apart) courtesy of Steve Lawrie, together with A1984 courtesy of Derek Harborne, and A3544, postally cancelled at Totton (mine).

A2017, A2057 and A2217 (C5R2) (200, 40 apart) courtesy of Steve Lawrie.

A2338 courtesy of Martien Blank and A4418 (C5R3) (2080 apart) courtesy of Steve Lawrie.

A1979 and A2059 (C5R4) courtesy of Steve Lawrie, A4419 (2360, 80 apart) courtesy of Andrew Higson. A2099 shown below also matches.

A2211 and A2371 (C6R1) (160 apart) courtesy of Steve Lawrie.

A2174 and A2414 (C6R4) (240 apart) courtesy of Steve Lawrie.

A2006 Courtesy of Steve Lawrie and A2166 (C7R1) (160 apart) courtesy of Mark Gibson.

A1968 Courtesy of Steve Lawrie and A6248 (C7R3) (4280 apart) courtesy of Martien Blank.

A2122 courtesy of capital-collectables on eBay,
with A2042 and A4722 (C8R2) (2600, 80 apart) courtesy of Steve Lawrie.
Note straight edges on the right of 2 of these. A2122 remains puzzling.

A7404 Courtesy of Steve Lawrie and A6244 (C8R4) (1160 apart) , now mine Ex-Andrew Higson.
Pairs with serial numbers 20 apart do not have matching flaws.
 |
 |
| A1993 (C2R3) - courtesy of Mike Jackson. | A2013 (C6R3) - courtesy of Martien Blank. |
Other non-matching pairs are 2115-2135, 2174-2194 and 5304-6244 which is 940 apart (47x20).
 |
 |
| A2200 (C1R5) - This is a recent acquisition and was the first example I had seen from Column 1. I show it here as column 1 is important in the following analysis. The selvedge proves it is from the left edge of the sheet. One of the problems with surface coating is that it is susceptible to damage by water or solvents. This has no gum, has some surface abrasion and a closed tear at the top. It has survived though, where apparently most did not. |
|
If we assume that each matching pair is from the same position on different sheets, then the difference between their
control numbers (assuming consistent numbering) must be a multiple of the number of stamps on the sheet.
The next step was to look at these differences:
It would seem that regardless of how they were sold to the public, they were printed and consistently numbered in sheets of 40 stamps.
From the horizontal pairs, we can see this was in 5 rows of 8 stamps per row.
This gave me the characteristic flaws of 14 out of the 40 stamps, or 35% of them.
To me the biggest difference was whether or not the stamps were included in booklets (I stand to be corrected).
If we assume that column-1 stamps are rare because they were not included in booklets, then other stamps not included in booklets would have equal scarcity.
If it was decided to have only one kind of booklet and to secure the stamps by the selvedge, then the most likely ones they chose would be these two.
Of these, the horizontal format is the most likely, otherwise it would be difficult to account for the number of row 1 and 2 stamps but no column 1 stamps.
With the horizontal format, there is still the problem of accounting for all the row-3 stamps we have with no column-1 stamps.
Another possibility is to have two types of booklet, one with a horizontal format, the other vertical:
Together these give 5 horizontal panes and 5 vertical panes from two sheets leaving 20 (including column 1) leftover stamps for sale over the counter.
An alternative would be these (or mirror images):
It still requires an explanation as to what happened to the column-1 stamps ?
However panes of 6 are selected, it leaves some loose stamps that still survived, why not column 1.
I have scans of only two intact pairs. There is no way to know if they were ever in booklets, but if the column-1 stamps are scarce
because they were not in booklets, then that implies that most of the stamps I have scans of, were from booklets.
A possibility that has to be considered is that the statement "reported to have been issued in booklets of 10 panes of six stamps"
was in error and should have been "reported to have been issued in booklets of 6 panes of ten stamps".
This would certainly be easier to manage with sheets of 8 x 5 stamps, but there is still the problem of the scarcity of column-1 stamps.
If both left and right sides were horizontally printed through the selvedge, but with no perforations vertically between the last stamp and sheet edge,
it may have been convenient to remove left and right columns and just use the middle 3 blocks of 10 stamps for booklets.
There is still no explanation though as to why column 8 has survived in preference to column-1.
Perhaps Column-1 was given to counter staff and did not generally get bought by the public to take away, whilst column-8 stamps were used as samples by salesmen.
Knowing the pattern makes it possible to predict which should match.
 |
 |
 |
| A6272 (C2R2) now one of mine. | A5312 (C2R2) courtesy of Paul & Les Bottomley. | A2032 (C2R2) courtesy of Auktionshaus Christoph Gärtner. |
These three are from the same position. Difficult to see if the last matches.

The system of numbering told me that these two formed a pair.
A5317, courtesy of Steve Lawrie, from the rare left side of the sheet, unused, digitally reunited with the used A5312 from above.
Used are almost as scarce as left side of sheet.
These pairs match well.
So do these.
 |
 |
 |
| A2146 (C3R1) Courtesy of capital-collectables |
A2226 (C3R1) Courtesy of Steve Lawrie. |
A3546 (C3R1) Courtesy of Martien Blank. |
Two more that should match.
 |
 |
| A2135 (C6R5) - Anonymous. | A9855 (C6R5) the highest number I have seen. courtesy of Auktionshaus Christoph Gärtner. |
Not very convincing, but likely.
 |
 |
| A2229 (C3R4) - From Langmead & Huggins book Fig.33 Courtesy of the Great Britain Philatelic Society. |
A6269 (C3R4) |
This is a good match.
 |
 |
| A2435 (C2R5) | A2115 (C2R5) - Anonymous |
The right-hand image is rather poor, but some features match.
 |
 |
 |
| A2065 (C4R5) capital-collectables on eBay. | A2425 (C4R5) courtesy of Mark Gibson. This should match the last one, A2345. |
A2345 (C4R5) courtesy of Edward Coombes. |
These have a rather conspicuous flaw to give them a match.
 |
 |
| A2092 (C6R2) one of mine. | A8852 (C6R2) courtesy of Steve Lawrie. |
These have a rather conspicuous flaw to give them a match.
There are 5 other scans of 6d stamps not yet shown, these are shown below.
 |
 |
 |
| A2023 (C4R3) courtesy of Steve Lawrie. | A2102 (C4R2) courtesy of Steve Lawrie. | A4110 (C3R5) courtesy of Steve Lawrie. |
 |
 |
| A2099 (a fourth C5R4) one of mine. | A2020 (C5R5) courtesy of Andrew Higson. |
To work that out from only 12 scans involved a lot of luck. (Now I have 18 scans)
Consecutive serial numbers are usually vertical pairs:
 |
| These seems to fit : A2464 (courtesy of Steve Lawrie) and A2465 (courtesy of Martien Blank) and A2466 (courtesy of Andrew Higson). They are the only vertically connecting stamps so far. |
Despite only having only 12 scans at the time of different 4d examples, I was lucky enough to find two matches.

A2466(courtesy of Andrew Higson) and A2340(courtesy of Mark Gibson) are 126 apart. this is (42 x 3), (21 x 6), or (7 x 18).
However, 18 stamps per sheet would put A2356 and 2392 in the same position and also A2315 and A2333. But neither seems to match well.
A2333 does match A2375 though.
 |
 |
| A2333 courtesy of Steve Lawrie. | A2375 |
These numbers are 42 apart, suggesting 6, 7 or 42 stamps per sheet.
 |
 |
| A2342 courtesy of Steve Lawrie. | A2468 courtesy of Andrew Higson. |
A new scan provides another match. These are 126 apart, or 3 x 42.
If there were only 6 or 7 stamps per sheet, I would have a lot more than 3 matches with 17 stamps.
The answer would indeed appear to be 42 stamps per sheet, since it is also compatible with the match above.
The next question is, is this 6 rows of 7 or 7 rows of 6? (assuming it isn't 14 x 3)


These are 7 apart, if there were 7 stamps to a column, they would be adjacent and the same height. They are clearly not the same height.
The stamps with edging on them shown below make it certain that these two are on the same sheet.
That means it must be 6 stamps to a column, i.e. 6 rows, and therefore 7 stamps to a row.
 |
 |
 |
 |
| A2315 courtesy of the late Mike Holt - It is the only one I've seen with a broken line under 'LIMITED'. |
A2354 courtesy of Steve Lawrie. | A2356 courtesy of Steve Lawrie. | A2358 |
Experience with the 6d makes me confident that these are on the edge of a sheet.
Although, considering the last 3 have to be on the edge of the same pane, it looks like some have been trimmed.
 |
| A2392 courtesy of Mark Gibson. |
This seems to show a straight edges on the left side like the 6d and 3d ones do.
This also though shows an indications of a single perforation on that side.
There is another constraint on the number of stamps per sheet:
 |
 |
 |
 |
| 4d control *A2466 on dull paper. | 4d control *A2468 on translucent paper. |
| Courtesy of Andrew Higson who remarks that for such close serial numbers, the paper and colour are very different. A2466 and A2468 are clearly from different sheets. Assuming an unbroken numbering sequence, A2466 would be the last in its sheet if there were 6 or 18 stamps per sheet. They would both be on the same sheet if it were 12, 20, 21, 24, 30, 32, 36, 40, 42, 46 or 48 stamps per sheet. This puts a fly in the ointment, as we have now concluded there are 42 stamps per sheet. We have to throw out our initial assumption. Things appear to be consistent up to A2375 that matches A2333, but then A2340 matches A2466, so it is hard to see how A2468 would be on another sheet ! |
|
This would give us:
 |
|
| A2364 - courtesy of Martien Blank. | A2358 |
| Were these once joined together ? | |
There is 2 other scan of a 4d stamps not yet shown, A2378 and A2383.
These are shown below.
 |
 |
| A2378 - courtesy of Steve Lawrie. | A2383 - courtesy of Steve Lawrie. |
I initially thought 28 stamps per sheet which would have been good for producing booklet panes.
The problem was that it would imply that I should have a lot of matching scans that do not in fact match.
I have only two scans of consecutive numbers of the 3d. Also (perhaps) one horizontal pair.
I do have several scans with matching flaws however:


A1379 courtesy Geoff Wright of Sandysstamps and A1463 (84 apart) - courtesy of Steve Lawrie.

A1320 courtesy of Steve Lawrie, and A1404 (84 apart) - courtesy of Mike Holt.

A1112 courtesy of Steve Lawrie and A1448 (336 apart) courtesy of Martien Blank.


A1144 (anonymous) and A1480 (336 apart) courtesy of Auktionshaus Christoph Gärtner.
I didn't expect to be able to match the image on the right, but the numbers said I should check against A1144. Here it is in the middle.
I subsequently got the last image, courtesy of Corinphila, another match.
| high | 1463 | 1404 | 1448 | 1480 |
|---|---|---|---|---|
| low | 1379 | 1320 | 1112 | 1144 |
| difference | 84 | 84 | 336 | 336 |
| interpretation-1 | 4 x 21 | 7 x 12 | 28 x 12 | 28 x 12 |
| interpretation-2 | 7 x 12 | 6 x 14 | 24 x 14 | 24 x 14 |
| interpretation-3 | 6 x 14 | 3 x 28 | 14 x 6 | 12 x 28 |
| interpretation-4 | 3 x 28 | 2 x 42 | 4 x 84 | 4 x 84 |
One of them could be mis-numbered, but the 6d stamps seem very consistent.
With just the first pair it looked like the early ones were in sheets of 40, but later ones were in sheets of 12 or 6.
Now though, the ranges overlap.
The first pair (A661/A1221) do not look very convincing, perhaps they are not really a match. What else do we have?
A1267 and A1262 (with selvedge) are just 5 apart.
If they were both from sheets with 5 stamps per column, then they should be a horizontal pair.

A1267 courtesy of Steve Lawrie and A1262 now mine, Ex-Andrew Higson.
Clearly they are not from the same row, they have different heights. If they were numbered like the 6d stamps, they did not have 6 stamps per column.
If there were 5 stamps per row, A1267 should also have selvedge.
The selvedge on A1262 (courtesy of Andrew Higson) has to be accounted for.
If they were all in sheets of 28, this would be the second stamp on its sheet.
A sheet starting with A1261 (following 105 sheets of 12) could be like this:
| R\C | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 1269 | 1265 | 1261 |
| 2 | 1270 | 1266 | 1262 |
| 3 | 1271 | 1267 | 1263 |
| 4 | 1272 | 1268 | 1264 |
The problem with this is that it puts 6 other pairs in the same locations that do not actually appear to match.
Indeed, my simulations suggest that to get only two matching pairs out of 22 stamps, there should be about 80 or so stamps per sheet.
A sheet starting with A1261 (following 45 sheets of 28) could be like this:
| R\C | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 1282 | 1275 | 1268 | 1261 |
| 2 | 1283 | 1276 | 1269 | 1262 |
| 3 | 1284 | 1277 | 1270 | 1263 |
| 4 | 1285 | 1278 | 1271 | 1264 |
| 2 | 1286 | 1279 | 1272 | 1265 |
| 3 | 1287 | 1280 | 1273 | 1266 |
| 4 | 1288 | 1281 | 1274 | 1267 |
This would put A1267 on the right edge under A1262. However it doesn't have selvedge !
This gives positions for the early 6d type on a 5 rows of 8 basis.
for the 3d it does the same for the first 31 sheets (1240 stamps) then switches to 12 stamps per sheet.
Enter a Control number to check
|
|
|
A1112 courtesy of Steve Lawrie and matching A1448 courtesy of Martien Blank from above, together with A1336 courtesy of Andrew Higson,
and now A1364. With 4 rows of 7 stamps, these would all be Col.3, Row 4.
The first two and last match, but not the third.


A1310 is courtesy of Derek Harborne and A1338 courtesy of Martien Blank. They do not appear to match.


A1395 is illustrated by Langmead and Huggins (colour plate 2) and is Courtesy of the Great Britain Philatelic Society, with A1423 courtesy of Mark Gibson.
With 4 rows of 7 stamps, these would both be Col.2, Row 3. They do not appear to match.

A661 and A1221 (560 apart) courtesy of Steve Lawrie. I originally matched these because of the bottom-right corner,
I am now inclined to think this similarity is a coincidence. There are differences.


A1357 courtesy of Steve Lawrie and A1469 courtesy of Mark Gibson.
With 4 rows of 7 stamps, these would both be Col.4, Row 1. They do not appear to match either.
A1463 and A1267 courtesy of Steve Lawrie, with A1379 courtesy Geoff Wright of Sandysstamps
With 4 rows of 7 stamps, these would all be Col.6, Row 3. Again, the first two match but not the third.


A1401 courtesy of Mark Gibson and A1429 courtesy of Steve Lawrie.
With 4 rows of 7 stamps, these would both be Col.7, Row 1. They look about as different as they can get.


Nothing in common and A1262 is clearly an edge stamp, A2382 courtesy of Steve Lawrie, is not.
The large number of false matches suggests that there are more stamps in the sheet.
But if there are more than 6 rows then A1267 will be in column 7 under A1262, but it does not have selvedge.
If we ignore the A661/A1221 match as being a coincidence, there is the possibility of 84 stamps per sheet.
If we keep 4 rows, then this would need 21 columns (3 panes of 7).
If there are 6 rows, then this would need 14 columns (2 panes of 7).
Enter a Control number to check
|
Enter a Control number to check
|

Here are A1463 and A1469. It's close and the straight edge on 1469 suddenly finds an explanation (which it doesn't in the other scenarios).
Looking at the other 3d examples with straight edges, A1221 and A1429 are at 7/3 and 14/1, both on the right sides (of a block of 7 columns) and both
having straight edges that side. A1386 is from 8/6 on the left side with that edge straight.
A bit much for a coincidence, each of the other scenarios get 1 out of 3 correct, but the fact of straight edges on 7/3 and 14/1 may be significant.
Admittedly someone could have snipped off perforations on a whim, but if not perhaps the sheets were actually 12 rows of 7 to make 84.
So does this pair fit together? What do you think ?
That would suggest that 12 rows of 7 stamps arranged in panes as shown (for the straight edges) as the most likely option.
Here is a potential fly in the ointment. The 3d is normally on yellow paper, but of variable transparency.
 |
 |
| 3d control A1262 (16/14/2 ?) | 3d control A1336 (16/2/4 ?) |
| Reverse of stamps shown above, courtesy of Andrew Higson. Are these from the same sheet? They were on different panes, could the different panes have been on different sheets of paper? A1379 (sheet 17) appears to be on the same kind of paper as A1336. There is a similar problem with the 4d stamps. The bottom-right corner of A1262 though looks a bit more translucent, perhaps some were affected by oil or something. |
|
This A1262 example presents another problem. It is very tall, how far apart were the rows of stamps?
It looks like it is from the top of a sheet but in our current scenario it isn't.
Here is another problem.
The stamp below presents something of an enigma. This is one of 6 scans I have between A1400 and A1430, but the others are all normal.
It is imperf. and surface coated rather than being on yellow paper. It was sold as a proof, presumably of surface coating. The number appears to have been random. There was almost certainly a real A1415. Anyone have it ?
The 3d and 4d were normally printed on coloured paper.
 |
 |
 |
| 3d control A1415 sold as a proof. | 3d control A1415 sold as a proof. | Back of 6d control A6244 surface coated sheet edge stamp |
| Courtesy of Andrew Higson. | One of mine. | |
One more fly to add to the ointment :
A4999, the highest number I've seen of these.

This should be on the right side of the sheet. Other stamps in that position have a straight edge on the right.
Is there a problem with this proposed arrangement? This is the highest number that I've seen for the 3d. Perhaps something changed,
perhaps they started perforating around the edges ? On the other hand it may have been torn from a stub on the left-hand side.
There are 5 other scans of 3d stamps not yet shown.
These are A1324, A1386, A1443, A2121 and A4853 and are shown below.



A1324 and A1386 (an edge stamp), and A4853 courtesy of Steve Lawrie.


A1443 (mine), and A2121 courtesy of Mark Gibson
More scans needed.
Later the design was changed, initially with manuscript controls.
 |
 |
 |
 |
 |
| 3d on blue-green paper, RH4 Number 240 |
6d on vermilion paper, RH5 Number 860 |
6d RH5 Number 427 |
6d RH5 Number 446 ? |
6d RH5 Number 363 changed to 863 ? |
| From Langmead & Huggins, Colour Plate 1, Courtesy of the Great Britain Philatelic Society. | Courtesy of Steve Lawrie. | |||
I have now one scan of the 3d, control 240, as illustrated in the Langmead and Huggins book.
This matches row 5 stamp 8 of the later type (see below), the last stamp on the 6th. sheet of 40.
240 is the correct control number for the last stamp on the sixth sheet.
6d Control 860 is illustrated by Langmead and Huggins and matches row 5, stamp 4, though 860 would be expected at row 3 stamp 4.
6d control 427 is a Group 2 stamp matching row 2 stamp 4 of the later type stamps, though 427 would be expected at row 4 stamp 3.
6d control 446 is a Group 2 stamp matching row 1 stamp 6 of the later type stamps.
6d control 863(?) is also a Group 2 stamp but matches row 3 stamp 5 of the later type stamps, though 863 would be expected at row 3 stamp 7.
It makes no difference to the 3d, it is still the last stamp in the sheet,
but now the 6d stamps numbered 860 and 863 are correct, but the last would need to be 417 to match.
Transitional VERTICAL numbering.
Enter a Control number to check
| Sheet (1+) | Row (1->5) | Column (1->8) |
|---|---|---|
| From Langmead & Huggins, Colour Plate 1. Courtesy of the Great Britain Philatelic Society. |
One of mine. | Courtesy of Roger de Lacy-Spencer. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 240 (6/5/8) | 4000 (100/5/8) | 1520 (38/5/8) | 6800 (170/5/8) |
The 6d stamps, though of the same type, appear to have had a different arrangement on the plate.
| From Langmead & Huggins, Colour Plate 1. Courtesy of the Great Britain Philatelic Society. |
One of mine. | Courtesy of the late Mike Holt. | Anonymous. |
 |
 |
 |
 |
| 860 (22/5/4) | 2836 (71/5/4) | 4036 (101/5/4) | 4436 (111/5/4) |
| Courtesy of Steve Lawrie. | One of mine. | Courtesy of Steve Lawrie. | Courtesy of Martien Blank. |
 |
 |
 |
 |
| 417 misnumbered? (11/2/4) | 3292 (83/2/4) | 3932 (99/2/4) | 3092 (78/2/4) |
| Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. | Courtesy of Andrew Higson. | One of mine. |
 |
 |
 |
 |
| 446 (12/1/6) | 3486 - 88/1/6 (Group 3) | 2806 - 71/1/6 (Group 3) | 3806 - 96/1/6 (Group 3) |
| Courtesy of Steve Lawrie. | Courtesy of Mark Gibson. | Courtesy of mirak5 on ebay. |
 |
 |
 |
| 863 (22/3/5) | 9141 (229/3/5) | 3141 (79/3/5) |
6d Group 2 stamps have the characteristic mark above 'ES' of 'MESSAGE' and extended bottom line of 'E' in 'CHIEF'.
There are matching flaws between the manuscript and later types, however the 6d later types share common flaws that do not appear to be on the manuscript types.
These presumably were picked up on a transfer from the manuscript type.
Additionally, and more importantly the later type appear to be in different positions.
This may account for the 'scrambled' Group arrangement of the later type.
The 3d later types may have been printed from the same plate as the manuscript 3d types.
More scans needed.
Despite L&H saying these are Perf. 12½, I make them Perf. 12
The controls were printed in either large or small type. The colours were changed to those below.
 |
 |
 |
 |
| Hiscocks H6 | Hiscocks H6a courtesy of Mark Gibson. | Hiscocks H7 | Hiscocks H7a |
In the beginning I had little in the way of multiples, re-joined pairs at best and it was painstaking to make a case for the sheet layouts.
Fortunately larger multiples have now come to light that make a simpler and more convincing case.
The block below is courtesy of Steve Lawrie.

The difference of 8 between the top stamps and the bottom, makes it clear that there were 8 stamps in a row. It also implies that this sheet ended with number 16440, so 16440 should be divisible by the number of stamps per sheet.
For a long time, it bothered me that I never saw a pair crossing the left-right division but, getting ahead a bit, the strip below does, though it is re-joined. I suspect that the complete sheets were routinely quartered before use.
| Re-joined strip of 4 courtesy of Andrew Higson. |
 |
| 4850 to 4853 are from row 2, columns 2 to 5 |
The next step is to determine the number of stamps (and thus rows) in a sheet.
As with the first series, matching flaws are needed.
I now have many choices, but this is a good example.
| Courtesy of Mark Gibson. | Anonymous | Anonymous. | Anonymous |
 |
 |
 |
 |
| 1569 (40/2/1) | 4529 (114/2/1) | 8249 (207/2/1) | 1693 (43/2/5) |
| high | 8249 | 4529 | 1693 | 4529 |
|---|---|---|---|---|
| low | 4529 | 1693 | 1569 | 1569 |
| difference | 3720 | 2836 | 124 | 2960 |
| interpretation | 93 x 40 | 709 x 4 | 31 x 4 | 74 x 40 |
| Position in sheet | - | - | - | - |
| Column (1-8) | - | - | - | - |
| Row (1-5) | - | - | - | - |
One thing that quickly became apparent is that there were slight differences between types.
1693 has an extra flaw (left of the 'L' corner) that the others do not have. It is from a different (though related) position.
I started to use the term 'alt' for alternative to indicate the similar ones.
Below is a more complete list of stamps like this:
| Row-2 PRIMARY flaws | ||||||||||||
All have the following flaws in common:
|
Controls: large 853, 1413, 1653, 1693, 3973, 4529, 4853, 4893 small 1569, 1649, 8209, 8249 These stamps are quite distinctive. Using my 'widget' at the bottom gives me: 853 = 22/2/5 1413 = 36/2/5 1569 = 40/2/1 1649 = 42/2/1 1653 = 42/2/5 1693 = 43/2/5 3973 = 100/2/5 4529 = 114/2/1 4853 = 122/2/5 4893 = 123/2/5 8209 = 206/2/1 8249 = 207/2/1 |
Splitting the two types gives:
|
|
Knowing there are 40 stamps per sheet and 8 stamps per row tells me that there are 5 rows per sheet.
I have broken the control number down into Sheet(1+), Row(1 to 5) and Column(1 to 8) using the 'widget' below.
Tha 'alt's are 4 columns away. The right and left halves of the sheet appear to be close copies of each other.
Notice that this works with large and small controls.
Images of all of these can be found under 'Row-2' lower down.
Enter a Control number to check
| Sheet (1+) | Row (1->5) | Column (1->8) |
|---|---|---|
I originally chose arbitrary groups until I understood the pattern. I will now list by Row Number / Stamp Number.
I have put a thick green line around some major characteristics and a thin one around lesser associated ones I have listed.
The magenta lines represent smaller ones I did not list. Smaller marks may be visible or not depending on under/over inking and age of the stone.
I have used green to indicate primary flaws in which case the blue indicates secondary flaws.
| Row-1 PRIMARY flaws All five have the following flaws in common:
|
| One of mine. | Courtesy of the late Mike Holt. | SECONDARY flaws | |
 |
 |
This pair have the following flaws in common that the other pairs do not have:
Row-1, Stamps-1 & 5 Controls: 885, 1481, 1485, 1685, 2085, 2845 small: 685, 10325 Using my 'widget' at the bottom gives me: 685 = 18/1/5 885 = 23/1/5 1481 = 38/1/1 1485 = 38/1/5 1685 = 43/1/5 2085 = 53/1/5 2845 = 72/1/5 10325 = 259/1/5 |
|
| 1481 (38/1/1) | 885 (23/1/5) | ||
| One of mine. | Courtesy of Steve Lawrie. | SECONDARY flaws | |
 |
 |
This pair have the following flaws in common that the other pairs do not have:
Row-1, Stamp-2 Controls: 1482, 1562, 4242 Using my 'widget' at the bottom gives me: 1482 = 38/1/2 1562 = 40/1/2 4242 = 107/1/2 . |
|
| 4242 (107/1/2) | 1562 (40/1/2) | ||
| One of mine. | Anonymous. | SECONDARY flaws | |
 |
 |
This pair have the following flaws in common that the other pairs do not have:
Row-1, Stamp-6 Controls: 206, 1286, 1646, 3966, 4886 Using my 'widget' at the bottom gives me: 206 = 6/1/6 1286 = 33/1/6 1646 = 42/1/6 3966 = 100/1/6 4886 = 123/1/6 A mark appears between 'LE' of 'TELEGRAPH' on 1646 and after. |
|
| 206 (6/1/6) | 1646 (42/1/6) | ||
| One of mine . | Courtesy of ibredguy.co.uk. | SECONDARY flaws | |
 |
 |
This pair have the following flaws in common: that the other pairs do not have:
Row-1, Stamps-3 & 7 Controls: 843, 1363, 1487, 1767, 2163, 2763, 4207, 4247 small 3887, 10327 Using my 'widget' at the bottom gives me: 843 = 22/1/3 1363 = 35/1/3 1487 = 38/1/7 1767 = 45/1/7 2163 = 55/1/3 2763 = 70/1/3 3887 = 98/1/7 4207 = 106/1/7 4247 = 107/1/7 10327 = 259/1/7 |
|
| 843 (22/1/3) | 4247 107/1/7) | ||
| One of mine. | One of mine. | SECONDARY flaws | |
 |
 |
Characteristics:
Row-1, Stamp-4 & 8 Controls: 928, 2124, 2444, 3164 small: 1648, 6164, 10328 Using my 'widget' at the bottom gives me: 928 = 24/1/8 1648 = 42/1/8 2124 = 54/1/4 2164 = 55/1/4 2444 = 62/1/4 6164 = 155/1/4 10328 = 259/1/8 |
|
| 2444 (62/1/4) | 10328 (259/1/8) |
| One of mine. | Courtesy of ibredguy.co.uk. | Courtesy of Steve Lawrie. |
 |
 |
 |
| 1481 (38/1/1) | 1482 (38/1/2) | 1562 (40/1/2) |
| One of mine. | Courtesy of Steve Lawrie. | One of mine. |
 |
 |
 |
| 4242 (107/1/2) | 843 (22/1/3) | 1363 (35/1/3) |
| Courtesy of Steve Lawrie. | One of mine. | Anonymous. | One of mine. |
 |
 |
 |
 |
| 2163 (55/1/3) | 2763 (70/1/3) | 2124 (54/1/4) | 2164 (55/1/4) |
| One of mine. | Courtesy of Martien Blank. | Courtesy of Steve Lawrie. | Courtesy of the late Mike Holt. |
 |
 |
 |
 |
| 2444 (62/1/4) | 6164 (155/1/4) | 685 (18/1/5) | 885 (23/1/5) |
| One of mine. | Courtesy John A. McCulloch, © 2010 ARR. | Courtesy of Steve Lawrie. |
 |
 |
 |
| 1485 (38/1/5) | 1685 (43/1/5) | 2085 (53/1/5) |
| Courtesy of ibredguy.co.uk. | Courtesy of Steve Lawrie. |
 |
 |
| 2845 (72/1/5) | 10325 (259/1/5) |
| One of mine. | Courtesy of Steve Lawrie. | Anonymous. |
 |
 |
 |
| 206 (6/1/6) | 1286 (33/1/6) | 1646 (42/1/6) |
| One of mine. | Courtesy of Steve Lawrie. | Courtesy of ibredguy.co.uk. | One of mine. |
 |
 |
 |
 |
| 3966 (100/1/6) | 4886 (123/1/6) | 1487 (38/1/7) | 1767 (45/1/7) |
| Courtesy of Mark Gibson. | Anonymous. | Courtesy of ibredguy.co.uk. | One of mine. |
 |
 |
 |
 |
| 3887 (98/1/7) small. | 4207 (106/1/7) | 4247 (107/1/7) | 10327 (259/1/7) |
| One of mine. | Courtesy of Steve Lawrie. | One of mine. |
 |
 |
 |
| 928 (24/1/8) | 1648 (42/1/8) | 10328 (259/1/8) |
These have a 'notch' on the left side of the 'T' corner, but it is higher than the other ones.
| Row-2 PRIMARY flaws All have the following flaws in common:
|
| Anonymous | Anonymous | SECONDARY flaws | |
 |
 |
This pair has the following flaws in common that the others do not have:
Row-2, Stamps-1 & 5 Controls: large 853, 1413, 1653, 1693, 3973, 4529, 4853, 4893 small 1569, 1649, 8209, 8249 These stamps are quite distinctive. Using my 'widget' at the bottom gives me: 853 = 22/2/5 1413 = 36/2/5 1569 = 40/2/1 1649 = 42/2/1 1653 = 42/2/5 1693 = 43/2/5 3973 = 100/2/5 4529 = 114/2/1 4853 = 122/2/5 4893 = 123/2/5 8209 = 206/2/1 8249 = 207/2/1 |
|
| 4529 (114/2/1) | 1693 (43/2/5) |
| One of mine. | Courtesy of Mark Gibson. | SECONDARY flaws | |
 |
 |
Characteristics:
Row-2, Stamps-2 & 6 Controls: 1450, 1490, 2130, 2134, 2690, 3974, 4254, 4850 small: 1654 These stamps are quite distinctive. Using my 'widget' at the bottom gives me: 1450 = 37/2/2 1490 = 38/2/2 1654 = 42/2/6 2130 = 54/2/2 2134 = 54/2/6 2690 = 68/2/2 3974 = 100/2/6 4254 = 107/2/6 4850 = 122/2/2 |
|
| 1450 (37/2/2) | 2134 (54/2/6) | ||
| Courtesy of Andrew Higson. | Courtesy of Andrew Higson. | SECONDARY flaws | |
 |
 |
Distinctive varieties of note:
Row-2, Stamps-3 & 7 Controls: 931, 1131, 2055, 4851, 4855 small: 10331, 10335 These stamps are quite distinctive. Using my 'widget' at the bottom gives me: 931 = 24/2/3 1131 = 29/2/3 2055 = 52/2/7 4851 = 122/2/3 4855 = 122/2/7 10331 = 259/2/3 10335 = 259/2/7 |
|
| 4851 (122/2/3) | 4855 (122/2/7) | ||
| Courtesy of ibredguy.co.uk. | Courtesy of the late Mike Holt. | SECONDARY flaws | |
 |
 |
These have the following flaws in common: that the others do not have:
Row-2, Stamp-4 Controls: large 972, 1372, 2012, 4216, 4772, 4852 small 5252, 10572, 24932 Using my 'widget' at the bottom gives me: 972 = 25/2/4 1372 = 35/2/4 2012 = 51/2/4 4612 = 116/2/4 4772 = 120/2/4 4852 = 122/2/4 5252 = 132/2/4 10572 = 265/2/4 24932 = 624/2/4 |
|
| 4612 (116/2/4) | 5252 (132/2/4) | ||
| Courtesy of the late Mike Holt. | Courtesy of ibredguy.co.uk. | SECONDARY flaws | |
 |
 |
These have the following flaws in common: that the others do not have:
Row-2, Stamp-8 Controls: large 1576, 1776, 2216, 2256, 4216, 4456, 4536 small 22656 Using my 'widget' at the bottom gives me: 1576 = 40/2/8 1776 = 45/2/8 2216 = 56/2/8 2256 = 57/2/8 4216 = 106/2/8 (2 copies) 4456 = 112/2/8 4536 = 114/2/8 22656 = 567/2/8 |
|
| 4216 (106/2/8) | 4456 (112/2/8) | ||
'r-dot' : The signature near the bottom is that of the Secretary and Manager Charles Curtoys.
There is a dot above the signature written as if the 'r' in 'Charles' was an 'i' so I will refer to it as the 'r-dot'
It can be clearly seen on the mint stamp above..
The 'r-dot' can help us. It can be as above or missing or over to the right near the 'l' of 'Charles'.
It depends on the stamp position, but not necessarily on the control number.
| Courtesy of Mark Gibson. | Anonymous. | Anonymous. | Anonymous. |
 |
 |
 |
 |
| 1569 (40/2/1) | 4529 (114/2/1) | 8209 (206/2/1) | 1649 (42/2/1) |
| Anonymous. | One of mine. | Courtesy of ibredguy.co.uk. | Courtesy of ibredguy.co.uk. |
 |
 |
 |
 |
| 8249 (207/2/1) | 1450 (37/2/2) | 1490 (38/2/2) | 2130 (54/2/2) |
| Anonymous. | Courtesy of Andrew Higson. |
 |
 |
| 2690 (68/2/2) | 4850 (122/2/2) |
| One of mine. | One of mine. | Courtesy of Andrew Higson. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 931 (24/2/3) | 1131 (29/2/3) | 4851 (122/2/3) | 10331 (259/2/3) |
| One of mine. | One of mine. | Courtesy of Steve Lawrie. |
 |
 |
 |
| 972 (25/2/4) | 1372 (35/2/4) | 2012 (51/2/4) |
| Courtesy of ibredguy.co.uk. | Courtesy of Mike Jackson. | Courtesy of Andrew Higson. |
 |
 |
 |
| 4612 (116/2/4) | 4772 (120/2/4) | 4852 (122/2/4) |
| Courtesy of the late Mike Holt. | Courtesy of Steve Lawrie. | One of mine. |
 |
 |
 |
| 5252 (132/2/4) | 10572 (265/2/4) | 24932 (624/2/4) - highest number |
| Courtesy of ibredguy.co.uk. | Courtesy of Steve Lawrie. |
 |
 |
| 853 (22/2/5) | 1413 (36/2/5) |
| Courtesy of Mike Jackson. | Anonymous. | Courtesy of Mark Talbot. | Courtesy of Andrew Higson. |
 |
 |
 |
 |
| 1653 (42/2/5) | 1693 (43/2/5) | 3973 (100/2/5) | 4853 (122/2/5) |
| One of mine. | One of mine. | Courtesy of Mark Gibson. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 4893 (123/2/5) | 1654 (42/2/6) | 2134 (54/2/6) | 3974 (100/2/6) |
| Courtesy of Steve Lawrie. | Reproduced with permission from http://www.stampboards.com | Courtesy of Andrew Higson. | One of mine. |
 |
 |
 |
 |
| 4254 (107/2/6) | 2055 (52/2/7) | 4855 (122/2/7) | 10335 (259/2/7) |
| One of mine. | Courtesy of ibredguy.co.uk. | One of mine. | One of mine. |
 |
 |
 |
 |
| 1576 (40/2/8) | 1776 (45/2/8) | 2216 (56/2/8) | 2256 (57/2/8) |
| Courtesy of Martien Blank. | Courtesy of the late Mike Holt. | Courtesy of ibredguy.co.uk. |
 |
 |
 |
| 4216 (106/2/8) used | 4216 (106/2/8) unused | 4456 (112/2/8) |
| Courtesy of Mark Gibson. | Courtesy of Stephen Gardner. |
 |
 |
| 4536 (114/2/8) | 22656 (567/2/8) |
| Row-3 PRIMARY flaws All four have the following flaws in common:
|
| One of mine. | One of mine. | SECONDARY flaws | |
 |
 |
There appear to be some flaws in common with all, but 3/5 has shared flaws not on 3/1 (red). Also 3/1 has a couple of flaws not on 3/5 (magenta).
Row-3, Stamps 1 and 5 Controls: 1537, 2137, 2141, 2781 Using my 'widget' at the bottom gives me: 1537 = 39/3/1 2137 = 54/3/1 2141 = 54/3/5 2781 = 70/3/5 |
|
| 1537 (39/3/1) | 2781 (70/3/5) | ||
| Courtesy of Stephen Gardner. | One of mine. | SECONDARY flaws | |
 |
 |
These have the following flaws :
Row-3, Stamps-2 & 6 Controls: 1498, 1978, 2142, 2262, 2782, 2822, 3182, 4862 small 1582, 15742 Using my 'widget' at the bottom gives me: 1498 = 38/3/2 1582 = 40/3/6 1978 = 50/3/2 2142 = 54/3/6 2262 = 57/3/6 2782 = 70/3/6 2822 = 71/3/6 3182 = 80/3/6 4862 = 122/3/6 15742 = 394/3/6 1498 and 1978 differ in having a scratch under the 'L' corner and a feint scratch across '90'. |
|
| 1978 (50/3/2) | 2822 (71/3/6) | ||
| Courtesy of Mark Gibson. | Anonymous | SECONDARY flaws | |
 |
 |
This pair have the following flaws in common that the other pairs do not have:
Row-3, Stamps-3 & 7 Controls: 1499, 2139, 2259, 2379, 2739, 2743, 4259, 4699 small 23499 Using my 'widget' at the bottom gives me: 1499 = 38/3/3 2139 = 54/3/3 2259 = 57/3/3 2379 = 60/3/3 2739 = 69/3/3 2743 = 69/3/7 4259 = 107/3/3 4699 = 118/3/3 23499 = 588/3/3 |
|
| 2739 (69/3/3) | 2743 (69/3/7) | ||
| One of mine | Courtesy of Chris Ceremuga. | SECONDARY flaws | |
 |
 |
These have the following flaws :
Row-3, Stamps-4 & 8 Controls: 340, 1580, 1860, 2140, 2780, 3660 small 1584, 2384 Using my 'widget' at the bottom gives me: 340 = 9/3/4 1580 = 40/3/4 1584 = 40/3/8 1860 = 47/3/4 2140 = 54/3/4 2384 = 60/3/8 2780 = 70/3/4 3660 = 92/3/4 |
|
| 3660 (92/3/4) | small 1584 (40/3/8) | ||
| One of mine. | One of mine. | One of mine. | One of mine. |
 |
 |
 |
 |
| 1537 (39/3/1) | 2137 (54/3/1) Note printing flaw. | 2141 (54/3/5) | 2781 (70/3/5) Note printing flaw. |
| One of mine. | Courtesy of Stephen Gardner. |
 |
 |
| 1498 (38/3/2) | 1978 (50/3/2) |
| Courtesy of Steve Lawrie. | Courtesy of Mike Jackson. | Courtesy of Steve Lawrie. |
 |
 |
 |
| 1582 (40/3/6) | 2142 (54/3/6) | 2262 (57/3/6) |
| Courtesy of Steve Lawrie. | One of mine. | One of mine. |
 |
 |
 |
| 2782 (70/3/6) | 2822 (71/3/6) | 3182 (80/3/6) |
| One of mine. | Courtesy of Steve Lawrie. |
 |
 |
| 4862 (122/3/6) | 15742 (394/3/6) |
| One of mine. | One of mine. | Courtesy of Steve Lawrie. |
 |
 |
 |
| 1499 (38/3/3) | 2139 (54/3/3) | 2259 (57/3/3) |
| Courtesy of Steve Lawrie. | Courtesy of Mark Gibson. | One of mine. |
 |
 |
 |
| 2379 (60/3/3) | 2739 (69/3/3) | 4259 (107/3/3) |
| Courtesy of Steve Lawrie. | Anonymous. | Anonymous. |
 |
 |
 |
| 4699 (118/3/3) | 23499 (588/3/3) | 2743 (69/3/7) |
| Courtesy of Mark Gibson. | Courtesy of Mike Jackson. | Courtesy of Steve Lawrie. |
 |
 |
 |
| 340 (9/3/4) | 1580 (40/3/4) | 1860 (47/3/4) |
| One of mine. | One of mine. | One of mine. |
 |
 |
 |
| 2780 (54/3/4) | 2780 (70/3/4) | 3660 (92/3/4) |
| Courtesy of Chris Ceremuga. | Courtesy of Steve Lawrie. |
 |
 |
| 1584 (40/3/8) | 2384 (60/3/8) |
| Row-4 PRIMARY flaws All four have the following flaws in common:
|
| Courtesy of Mark Gibson. | One of mine . | SECONDARY flaws | |
 |
 |
This pair have the following flaws in common:
Row-4, Stamp-1 Controls: 265, 945, 1105, 1345, 1825, 2065, 2265, 3985, 4705 small: 1625, 13825, 16665 Using my 'widget' at the bottom gives me: 265 = 7/4/1 945 = 24/4/1 1105 = 28/4/1 1345 = 34/4/1 1625 = 41/4/1 1825 = 46/4/1 2065 = 52/4/1 2265 = 57/4/1 3985 = 100/4/1 4705 = 118/4/1 13825 = 346/4/1 16665 = 417/4/1 |
|
| 1105 (28/4/1) | 1625 (small) (41/4/1) |
| One of mine. | Courtesy of Martien Blank. | SECONDARY flaws | |
 |
 |
This pair have the following flaws in common:
Row-4, Stamps-4 & 8 Controls: 988, 1712, 1872, 2148, 2152 small 1588 Using my 'widget' at the bottom gives me: 988 = 25/4/4 1588 = 40/4/4 1712 = 43/4/8 1872 = 47/4/8 2148 = 54/4/4 2152 = 54/4/8 4188 = 105/4/4 |
|
| 2148 (54/4/4) | 1872 (47/4/8) | ||
| Anonymous. | One of mine. | SECONDARY flaws | |
 |
 |
This pair have the following flaws in common:
Row-4, Stamp-5 Controls: 269, 2029, 4629 small 1589 Using my 'widget' at the bottom gives me: 269 = 7/4/5 1589 = 40/4/5 2029 = 51/4/5 4629 = 116/4/5 |
|
| small 1589 (40/4/5) | 269 (7/4/5) | ||
| Courtesy of Mark Gibson. | Anonymous. | SECONDARY flaws | |
 |
 |
This pair have the following flaws in common:
Row-4, Stamps-3 & 7 Controls: 467, 1507, 1551, 2431, 2471, 4911 small: 10867, 22231 Using my 'widget' at the bottom gives me: 467 = 12/4/3 1507 = 38/4/3 1551 = 39/4/7 2431 = 61/4/7 2471 = 62/4/7 4911 = 123/4/7 10867 = 272/4/3 22231 = 556/4/7 |
|
| 467 (12/4/3) this is the one illustrated by Hiscocks. | 1551 (39/4/7) | ||
| Courtesy of the late Mike Holt. | Courtesy of ibredguy.co.uk. | Courtesy of Mark Gibson. | One of mine. |
 |
 |
 |
 |
| 265 (7/4/1) | 945 (24/4/1) | 1105 (28/4/1) | 1345 (34/4/1) |
| One of mine. | Courtesy of Steve Lawrie. | Courtesy of Mark Gibson. | Courtesy of Andrew Higson. |
 |
 |
 |
 |
| 1625 (41/4/1) | 1825 (46/4/1) | 2065 (52/4/1) | 2265 (57/4/1) |
| Courtesy of Steve Lawrie. | Courtesy of Mark Gibson. | Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 3985 (100/4/1) | 4705 (118/4/1) | 13825 (346/4/1) | 16665 (417/4/1) |
| One of mine. | Courtesy of Mark Gibson. | Anonymous. | Anonymous. |
 |
 |
 |
 |
| 269 (7/4/5) | 2029 (51/4/5) | 4629 (116/4/5) | 1589 (40/4/5) |
| Courtesy of ibredguy.co.uk. | Anonymous. | One of mine. |
 |
 |
 |
| 906 (23/4/2) | 1106 (28/4/2) | 1506 (38/4/2) |
| Courtesy of Steve Lawrie. | One of mine. | Courtesy of Steve Lawrie. |
 |
 |
 |
| 2466 (62/4/2) | 4226 (106/4/2) | 10866 (272/4/2) |
| One of mine. | Courtesy of the late Mike Holt. |
 |
 |
| 1390 (35/4/6) | 4910 (123/4/6) |
| Courtesy of Mark Gibson. | One of mine. | One of mine. |
 |
 |
 |
| 467 (12/4/3) | 1507 (38/4/3) | 10867 (272/4/3) |
| Anonymous | One of mine. | Courtesy of Mark Gibson. |
 |
 |
 |
| 1551 (39/4/7) | 2431 (61/4/7) | 2471 (62/4/7) |
| One of mine. | Courtesy of Steve Lawrie. |
 |
 |
| 4911 (123/4/7) | 22231 (556/4/7) |
| Courtesy of Steve Lawrie. | Courtesy of Martien Blank. | One of mine. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 988 Group (25/4/4) | 1588 Group (40/4/4) | 2148 Group (54/4/4) | 4188 Group (105/4/4) |
| Anonymous. | Courtesy of Martien Blank. | Courtesy of Mark Gibson. |
 |
 |
 |
| 1712 (43/4/8) | 1872 (47/4/8) | 2152 (54/4/8) |
| Row-5 PRIMARY flaws All have the following flaws in common:
|
| Courtesy of Mark Talbot. | One of mine. | SECONDARY flaws | |
 |
 |
Flaws in common : (the first 3 are also on stamp 5/5)
Row-5, Stamp-1 Controls: 2313, 4193, 4633 Using my 'widget' at the bottom gives me: 2313 = 58/5/1 4193 = 105/5/1 4633 = 116/5/1 |
|
| 2313 (58/5/1) | 4193 (105/5/1) |
| Anonymous. | One of mine. | SECONDARY flaws | |
 |
 |
Flaws in common :
Row-5, Stamps-2 & 6 Controls: 954, 998, 1238, 1518, 1558, 2594, 4194 Using my 'widget' at the bottom gives me: 954 = 24/5/2 998 = 25/5/6 1238 = 31/5/6 1518 = 38/5/6 1558 = 39/5/6 2594 = 65/5/2 4194 = 105/5/2 |
|
| 954 (23/5/2) | 1238 (31/5/6) | ||
| Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. | SECONDARY flaws | |
 |
 |
Characteristics :
Row-5, Stamps-3 & 7 Controls: 915, 1315, 1355, 1439, 1599, 2635, 4199 small: 6799, 10559, 17679, 20755 Using my 'widget' at the bottom gives me: 915 = 23/5/3 1315 = 33/5/3 1355 = 34/5/3 2635 = 66/5/3 1439 = 36/5/7 1599 = 40/5/7 4199 = 105/5/7 6799 = 170/5/7 10559 = 264/5/7 17679 = 442/5/7 20755 = 519/5/3 |
|
| 915 (23/5/3) | 10559 (264/5/7) | ||
| Courtesy of the late Mike Holt. | One of mine. | SECONDARY flaws | |
 |
 |
Flaws in common :
Row-5, Stamp-5 Controls: 637, 1557, 2557, 4477 small 2357 These two stamps are very distinctive. Using my 'widget' at the bottom gives me: 637 = 16/5/5 1557 = 39/5/5. 2357 = 59/5/5. 2557 = 64/5/5. 4477 = 112/5/5. |
|
| 637 (16/5/5) | 1557 (39/5/5) | ||
| Courtesy of ibredguy.co.uk. | One of mine. | SECONDARY flaws | |
 |
 |
Flaws in common :
Row-5, Stamps-4 & 8 Controls: 1520, 1920, 4000, 4556, 4880 (small) 1596, 6800, 19876 Manuscript 240 (L&H on Plate 1) Using my 'widget' at the bottom gives me: 240 = 6/5/8 1520 = 38/5/8 1596 = 40/5/4 1920 = 48/5/8. 4000 = 100/5/8. 4556 = 114/5/4 4880 = 122/5/8. 6800 = 170/5/8. 19876 = 497/5/4 Surprisingly the manuscript control and large controls were consistent! 6800 appears to have had the number corrected. |
|
| small 19876 (497/5/4) | 4000 (100/5/8) | ||
| Courtesy of Mark Talbot. | One of mine. | One of mine. |
 |
 |
 |
| 2313 (58/5/1) | 4193 (105/5/1) | 4633 (116/5/1) |
| Courtesy of the late Mike Holt. | One of mine. | One of mine. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 637 (16/5/5) | 1557 (39/5/5) | 2357 (59/5/5) | 2557 (64/5/5) |
| Courtesy of Steve Lawrie. | Anonymous. | One of mine. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 4477 (112/5/5) | 954 ( 24/5/2) | 2594 ( 65/5/2) | 4194 ( 105/5/2) |
| One of mine. | One of mine. | Courtesy of ibredguy.co.uk. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 998 (25/5/6) | 1238 (31/5/6) | 1518 (38/5/6) | 1558 (39/5/6) |
| Courtesy of Steve Lawrie. | One of mine. | Courtesy of Mark Gibson. |
 |
 |
 |
| 915 (23/5/3) | 1315 (33/5/3) (damaged) | 1355 (34/5/3) |
| Anonymous. | Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. |
 |
 |
 |
| 2635 (66/5/3) | 20755 (519/5/3) | 1439 (36/5/7) |
| One of mine. | Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 1599 (40/5/7) | 4199 (105/5/7) | 6799 (170/5/7) | 10559 (264/5/7) - with 1886 postal cancel |
| Courtesy of Andrew Higson. | Courtesy of Mark Gibson. | One of mine. | Courtesy of ibredguy.co.uk. |
 |
 |
 |
 |
| 17679 (442/5/7) | 1596 (40/5/4) | 4556 (114/5/4) | 19876 (497/5/4) |
| One of mine. | Anonymous. | One of mine. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 1520 (38/5/8) | 1920 (48/5/8) | 4000 (100/5/8) | 6800 (170/5/8) |
 |
| 4879 is 122/5/7 and 4880 is 122/5/8 Unfortunately I do not know the source of this scan, anyone recognise it? I would like to give credit and perhaps get a better scan. These are also nearly the highest control numbers I have seen for these. |
| Re-joined strip of 3 courtesy of Andrew Higson. | ||
 |
||
| 2806 is Row-1, stamp 6 | 2807 is Row-1, stamp 7 | 2808 is Row-1, stamp 8 |
 |
|||
| 4501 is Row-3, stamp 5 | 4502 is Row-3, stamp 6 | 4503 is Row-3, stamp 7 | 4504 is Row-3, stamp 8 |
This is a reconstructed strip, held together at the back. These, like many of the others still have full gum despite being cancelled. It appears that they were generally pre-cancelled.
Until recently, the lack of any blocks and rarity of even pairs made this much more difficult.
This scan kindly provided by Martien Blank has confirmed much of the 'detective work'.
It certainly makes it clear that there were 8 stamps per row.

I will refer to this in the text as the 'MB-block'.
The arrangement of the 3d plate was fairly simple with the whole of each row derived from the same prototype (Group).
I expected the same of the 6d, but it was clearly not the case. some features on stamps also appear to have 'faded' over time.
See Row-1, stamp 1 , Row-2, stamp 1 , Row-4, stamp 2 and Row-5, stamp 7
I also had an expectation that some may have been printed as booklet panes.
Despite looking for evidence of this, I have to conclude that all the examples I have seen were printed in sheets of 40 stamps as with the 3d stamps.
The large and small controls fit the same pattern, but some slight differences suggest some plate-cleaning at some stage.
I have only scans of two examples of the earlier manuscript controls which are very similar to the 'Group 2' stamps below.
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 |
| R1/C1 | R1/C2 | R1/C3 | R1/C4 | R1/C5 | R1/C6 | R1/C7 | R1/C8 | |
| R2/C1 | R2/C2 | R2/C3 | R2/C4 | R2/C5 | R2/C6 | R2/C7 | R2/C8 | |
| R3/C1 | R3/C2 | R3/C3 | R3/C4 | R3/C5 | R3/C6 | R3/C7 | R3/C8 | |
| R4/C1 | R4/C2 | R4/C3 | R4/C4 | R4/C5 | R4/C6 | R4/C7 | R4/C8 | |
| R5/C1 | R5/C2 | R5/C3 | R5/C4 | R5/C5 | R5/C6 | R5/C7 | R5/C8 |
It is possible that the layout was intended to be the same as with the 3d stamps. My suspicion is as follows:
Two intermediate stones of 4 stamps derived from the same prototype (a manuscript type ?) were prepared,
but instead of the pairs staying together in the same finished row, they got mixed up.
It is possible that the manuscript type were in booklets of six and that five of these were used as prototypes for the later plates of 40.
With the manuscript types being so rare though, this has to remain conjecture.
| Row-1 PRIMARY flaws |
| Anonymous. | One of mine. | SECONDARY flaws | |
 |
 |
Common features:
Row-1, Stamp 1 Controls: 1681, 3961 small: 2121, 11961, 15081, 15841 Using my 'widget' at the bottom gives me: 1681 = 43/1/1 2121 = 54/1/1 3961 = 100/1/1 11961 = 300/1/1 15081 = 378/1/1 15841 = 397/1/1 On 1681, you can see the white marks in the 'L' corner of the stamp below. That is 1689. |
|
| 1681 | 2121 (small) | ||
| One of mine. | One of mine. | SECONDARY flaws | |
 |
 |
These have the following flaws in common:
Row-1, Stamp 2 Controls: 4002 small: 2562, 37882 Using my 'widget' at the bottom gives me: 2562 = 65/1/2 4002 = 101/1/2 37882 = 948/1/2 37882 was cancelled by favour in Totton, 1956. (despite the fact that it was already used) |
|
| 4002 | 37882 | ||
| Courtesy of Mark Gibson. | Anonymous. | SECONDARY flaws | |
 |
 |
These are similar to Row-1, stamp 1 above.
Row-1, Stamp 3 Controls: 2843, 3363, 4843 small 8283, 34683 Using my 'widget' at the bottom gives me: 2843 = 72/1/3 3363 = 85/1/3 4843 = 122/1/3 8283 = 208/1/3 34683 = 868/1/3 |
|
| 3363 | 8283 (small) | ||
| One of mine. | Courtesy of Mark Gibson. | SECONDARY flaws | |
 |
 |
These have the following flaws in common:
Row-1, Stamp 4 Controls: 524, 3684 small 21444 Using my 'widget' at the bottom gives me: 524 = 14/1/4 3684 = 93/1/4 21444 = 537/1/4 |
|
| 524 | 21444 (small) | ||
| One of mine. | Courtesy of Mark Gibson. | SECONDARY flaws | |
 |
 |
This is similar to Row-3 stamp 1 but without the join between 'Ch' of 'Charles'.
Row-1, Stamp 5 Controls: 3125, 3805, 4005 Small: 37885 Using my 'widget' at the bottom gives me: 3125 = 79/1/5 3805 = 96/1/5 4005 = 101/1/5 37885 = 948/1/5 3805 adjoins 3806 below. 37885 adjoins 37886 below. |
|
| 37885 | 3805 | ||
| Courtesy of Steve Lawrie. | One of mine. | SECONDARY flaws | |
 |
 |
These have the following flaws in common.
Row-1, Stamp 6 Controls: 2806, 3486, 3806 Small: 37886 Using my 'widget' at the bottom gives me: 2806 = 71/1/6 3486 = 88/1/6 3806 = 96/1/6 37886 = 948/1/6 2806 forms a strip with 2807 and 2808 3806 adjoins 3805 above. |
|
| 3486 | 3806 | ||
| Courtesy of Steve Lawrie. | Courtesy of Andrew Higson. | SECONDARY flaws | |
 |
 |
This shares the green flaws with 1/6 above. It shares the light blue flaws with 3/3 below, and has its own flaws shown in magenta.
Row-1, Stamp 7 Controls: 1687, 2807, 4847 small: 31847 Using my 'widget' at the bottom gives me: 1687 = 43/1/7 2807 = 71/1/7 4847 = 122/1/7 31847 = 797/1/7 2807 forms a strip with 2806 and 2808 1687 shows part of the 2/7 stamp below with a frame-break in the right corner. |
|
| 1687 | 2807 | ||
| Courtesy of Andrew Higson. | Anonymous. | SECONDARY flaws | |
 |
 |
Characteristics:
|
|
| 2808 | |||
| Anonymous. | One of mine. | Courtesy of Mark Gibson. |
 |
 |
 |
| 1681 - 43/1/1 (Group 4) | 2121 - 54/1/1 (Group 4) | 3961 - 100/1/1 (Group 4) |
| Anonymous. | Anonymous. | Courtesy of Ray Cobley. |
 |
 |
 |
| 11961 - 300/1/1 (Group 4) | 15081 - 378/1/1 (Group 4) | 15841 - 397/1/1 (Group 4) |
| Courtesy of ibredguy.co.uk. | One of mine. | One of mine. |
 |
 |
 |
| 2562 - 65/1/2 (Group 4) | 4002 - 101/1/2 (Group 4) | 37882 - 948/1/2 (Group 4) |
| Courtesy of Mike Jackson. | Courtesy of Mark Gibson. | Courtesy of Steve Lawrie. | Anonymous. |
 |
 |
 |
 |
| 2843 - 72/1/3 (Group 4) | 3363 - 85/1/3 (Group 4) | 4843 - 122/1/3 (Group 4) | 8283 - 208/1/3 (Group 4) |
| One of mine. | One of mine. | Courtesy of Steve Lawrie. | Courtesy of Mark Gibson. |
 |
 |
 |
 |
| 34683 - 868/1/3 (Group 4) | 524 - 14/1/4 (Group 4) | 3684 - 93/1/4 (Group 4) | 21444 - 537/1/4 (Group 4) |
| One of mine. | Courtesy of Mark Gibson. | One of mine. | One of mine. |
 |
 |
 |
 |
| 3125 - 79/1/5 (Group 3) | 3805 - 96/1/5 (Group 3) | 4005 - 101/1/5 (Group 3) | 37885 - 948/1/5 (Group 3) |
| Courtesy of Andrew Higson. | Courtesy of Steve Lawrie. | One of mine. | One of mine. |
 |
 |
 |
 |
| 2806 - 71/1/6 (Group 3) | 3486 - 88/1/6 (Group 3) | 3806 - 96/1/6 (Group 3) | 37886 - 948/1/6 (Group 3) |
| Courtesy of Steve Lawrie. | Courtesy of Andrew Higson. | One of mine. | Courtesy of ibredguy.co.uk. |
 |
 |
 |
 |
| 1687 - 43/1/7 (Group 3) | 2807 - 71/1/7 (Group 3) | 4847 - 122/1/7 (Group 3) | 31847 - 797/1/7 (Group 3) |
| Courtesy of Andrew Higson. | Courtesy of Mike Jackson. |
 |
 |
| 2808 - 71/1/8 (Group 3) | 4528 - 114/1/8 (Group 3) |
| Row 2 PRIMARY flaws |
| Courtesy of the late Mike Holt. | Courtesy of Mark Gibson. | SECONDARY flaws | |
 |
 |
For some reason these are very similar to 3/5. Common features:
Row-2, Stamp 1 Controls: 1689, 4809 small 2929, 37889 Using my 'widget' at the bottom gives me: 1689 = 43/2/1 2929 = 74/2/1 4809 = 121/2/1 37889 = 948/2/1 1689 adjoins 1681. At the bottom can be seen a frame break on the Row-3, stamp 1 stamp below. |
|
| 2929 (small) | 4809 |
| One of mine. | Courtesy of Chris Ceremuga. | SECONDARY flaws | |
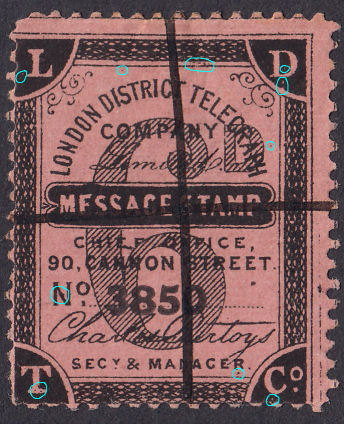 |
 |
Features :
small 25090. Using my 'widget' at the bottom gives me: 3850 = 97/2/2 25090 = 628/2/2 |
|
| 3850 | small 25090 | ||
| Anonymous. | Courtesy of Steve Lawrie. | SECONDARY flaws | |
 |
 |
These are similar to 3/6 and have the following flaws in common:
small: 31811, 37891 Using my 'widget' at the bottom gives me: 3411 = 86/2/3 4491 = 113/2/3 4971 = 125/2/3 31811 = 796/2/3 37891 = 948/2/3 |
|
| 4971 | 37891 | ||
| One of mine. | Courtesy of Steve Lawrie. | SECONDARY flaws | |
 |
 |
These have the following features:
small: 8212, 34252 Using my 'widget' at the bottom gives me: 2972 =75/2/4 3092 =78/2/4 3292 =83/2/4 3932 =99/2/4 8212 =206/2/4 9372 =235/2/4 34252 =857/2/4 3292 adjoins 3293 below. |
|
| 3292 | 3932 | ||
| One of mine. | Courtesy of ibredguy.co.uk. | SECONDARY flaws | |
 |
 |
These have the following flaws in common.
Row-2, Stamp 5 Controls: 3133, 3293, 3733, 3853, 4813, 4893, 8093 small 39773 Using my 'widget' at the bottom gives me: 3133 = 79/2/5 3293 = 83/2/5 3733 = 94/2/5 3853 = 97/2/5 4813 = 121/2/5 4893 = 123/2/5 8093 = 203/2/5 39773 = 995/2/5 3141 fits below 3133 3293 adjoins 3292 above. |
|
| 3853 | 3733 |
| One of mine. | SECONDARY flaws | |
 |
This has the following flaws in common with 4/6.
Row-2, Stamp 6 Controls: 1694 Using my 'widget' at the bottom gives me: 1694 = 43/2/6 On 1694, the top of a Row-3, stamp 6 can be seen at the bottom. |
|
| 1694 |
| Courtesy of Mark Gibson. | Courtesy of ibredguy.co.uk. | SECONDARY flaws | |
 |
 |
These have the following features:
Row-2, Stamp 7 Controls: 495, 2975, 3375, 4175, 4335, 4735 small: 15815, 37895 Using my 'widget' at the bottom gives me: 495 = 13/2/7 2975 = 75/2/7 3375 = 85/2/7 4175 = 105/2/7 4335 = 109/2/7 4735 = 119/2/7 15815 = 396/2/7 37895 = 948/2/7 15815 adjoins 15816 below. |
|
| 3375 | 4735 | ||
| Courtesy of Mike Jackson. | Courtesy of Steve Lawrie. | SECONDARY flaws | |
 |
 |
These have similarities with 4/8 and the following additional flaws:
Row-2, Stamp 8 Controls: 4016 small: 1376, 13136, 15816, 15856, 38056 Using my 'widget' at the bottom gives me: 1376 = 35/2/8 4016 = 101/2/8 13136 = 329/2/8 15816 = 396/2/8 15856 = 397/2/8 38056 = 952/2/8 15816 adjoins 15815 above. |
|
| 4016 | 15816 |
| Anonymous. | Courtesy of the late Mike Holt. | Courtesy of Mark Gibson. | One of mine. |
 |
 |
 |
 |
| 1689 - 43/2/1 (Group 2) | 2929 - 74/2/1 (Group 2) | 4809 - 121/2/1 (Group 2) | 37889 - 948/2/1 (Group 2) |
| One of mine. | Courtesy of Steve Lawrie. |
 |
 |
| 3850 - 97/2/2 (Group 2) | 3411 - 86/2/3 (Group 2) |
| One of mine. | Anonymous. | Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 4491 - 113/2/3 (Group 2) | 4971 - 125/2/3 (Group 2) | 31811 - 796/2/3 (Group 2) | 37891 - 948/2/3 (Group 2) |
| One of mine. | Courtesy of Martien Blank. | One of mine. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 2972 - 75/2/4 (Group 2) | 3092 - 78/2/4 (Group 2) | 3292 - 83/2/4 (Group 2) | 3932 - 99/2/4 (Group 2) |
| One of mine. | One of mine. | Courtesy of Steve Lawrie. |
 |
 |
 |
| 8212 - 206/2/4 (Group 2) | 9372 - 235/2/4 (Group 2) | 34252 - 857/2/4 (Group 2) |
| Courtesy of Mark Gibson. | Anonymous. | Courtesy of ibredguy.co.uk. | One of mine. |
 |
 |
 |
 |
| 3133 - 79/2/5 (Group 1) | 3293 - 83/2/5 (Group 1) | 3733 - 94/2/5 (Group 1) | 3853 - 97/2/5 (Group 1) |
| Courtesy of Steve Lawrie. | One of mine. | Courtesy of the late Mike Holt. | Anonymous. |
 |
 |
 |
 |
| 4813 - 121/2/5 (Group 1) | 4893 - 123/2/5 (Group 1) | 8093 - 203/2/5 (Group 1) | 39773 - 995/2/5 (Group 1) |
| One of mine. |
 |
| 1694 - 43/2/6 (Group 1) |
| Courtesy of Steve Lawrie. | One of mine. | Courtesy of Mark Gibson. | One of mine. |
 |
 |
 |
 |
| 495 - 13/2/7 (Group 1) | 2975 - 75/2/7 (Group 1) | 3375 - 85/2/7 (Group 1) | 4175 - 105/2/7 (Group 1) |
| Courtesy of Martien Blank. | Courtesy of ibredguy.co.uk. | Courtesy of Mike Jackson. | One of mine. |
 |
 |
 |
 |
| 4335 - 109/2/7 (Group 1) | 4735 - 119/2/7 (Group 1) | 15815 - 396/2/7 (Group 1) | 37895 - 948/2/7 (Group 1) |
| Courtesy of Martien Blank. | Courtesy of Mike Jackson. | Courtesy of Martien Blank. |
 |
 |
 |
| 1376 - 35/2/8 (Group 1) | 4016 - 101/2/8 (Group 1) | 13136 - 329/2/8 (Group 1) |
| Courtesy of Steve Lawrie. | One of mine. | Courtesy of Andrew Higson. |
 |
 |
 |
| 15816 - 396/2/8 (Group 1) | 15856 - 397/2/8 (Group 1) | 38056 - 952/2/8 (Group 1) |
| Row-3 PRIMARY flaws |
| Anonymous. | Courtesy of Steve Lawrie. | SECONDARY flaws | |
 |
 |
These have the following flaws in common:
Row-3, Stamp 1 Controls: 3697,3737,3817,3977,4337,4977 small: 32137, 39857 Using my 'widget' at the bottom gives me: 3697 = 93/3/1 3737 = 94/3/1 3817 = 96/3/1 3977 = 100/3/1 4337 = 109/3/1 4977 = 125/3/1 21457 = 537/3/1 32137 = 804/3/1 39857 = 997/3/1 See also 3733 at Row-2, stamp 5 above, which is similarly centred to 3737. |
|
| 3737 | 32137 | ||
| One of mine. | Courtesy of Mark Gibson. | SECONDARY flaws | |
 |
 |
These have the following flaws in common:
Row-3, Stamp 2 Controls: 3418, 4218 small 36658 These stamps are quite distinctive. Using my 'widget' at the bottom gives me: 3418 = 86/3/2 4218 = 106/3/2 36658 = 917/3/2 |
|
| 3418 | 36658 (small) |
| Courtesy John A. McCulloch, © 2010 ARR. | Courtesy of Andrew Ridley. | SECONDARY flaws | |
 |
 |
These have the following features in common:
Row-3, Stamp 3 Controls: 1699, 1899 small 8019, 13779, 37899 Using my 'widget' at the bottom gives me: 1699 = 43/3/3 1899 = 48/3/3 8019 = 201/3/3 13779 = 345/3/3 37899 = 948/3/3 1699 and 1899 have fresh looking scratches (as marked) and marks under 'M' of 'MESSAGE' They also show the top of Row-4 stamps below. 37899 adjoins 37891 above. |
|
| 37899 | 1899 | ||
| One of mine. | Anonymous. | SECONDARY flaws | |
 |
 |
Characteristic flaws:
Row-3, Stamp 4 Controls: 500, 2140 Using my 'widget' at the bottom gives me: 500 = 13/3/4 2140 = 54/3/4 500 adjoins 501(below) and 508. |
|
| 500 | 2140 | ||
| One of mine. | Courtesy of Mark Gibson. | SECONDARY flaws | |
 |
 |
For some reason these are very similar to 2/1. Common features:
Row-3, Stamp 5 Controls: 461, 501, 3141, 4501 small: 9141 Using my 'widget' at the bottom gives me: 461 = 12/3/5 501 = 13/3/5 3141 = 79/3/5 4501 = 113/3/5 9141 = 229/3/5 The mark circled in magenta is on 461, 501, 3141 and 4501, but cannot be seen on 9141. 3141 fits below 3133 at 2/5 above. |
|
| 501 | 9141 (small) |
| Courtesy of Mark Gibson. | Anonymous. | SECONDARY flaws | |
 |
 |
These are similar to 2/3 and have the following flaws in common:
small 13422, 15102 Using my 'widget' at the bottom gives me: 2102 = 53/3/6 3942 = 99/3/6 4502 = 113/3/6 13422 = 336/3/6 15102 = 378/3/6 |
|
| 15102 (small) | 1663 booklet | ||
| Courtesy of Mark Gibson. | One of mine. | SECONDARY flaws | |
 |
 |
Features :
small 37903 Using my 'widget' at the bottom gives me: 1663 = 42/3/7 4503 = 113/3/7 4583 = 115/3/7 37903 = 948/3/7 |
|
| 1663 | 4583 | ||
| One of mine. | Courtesy of Steve Lawrie. | SECONDARY flaws | |
 |
 |
These have the following flaws in common with 3/6 above :
small: 37904 Using my 'widget' at the bottom gives me: 424 = 11/3/8 2984 = 75/3/8 4504 = 113/3/8 4864 = 122/3/8 4944 = 124/3/8 37904 = 948/3/8 2984 has selvedge at the right and cannot be booklet. Stamp 4944 shows the mark under the 'Co' corner of the stamp above. |
|
| 424 | 4864 | ||
| One of mine. | Anonymous. | One of mine. |
 |
 |
 |
| 3697 - 93/3/1 (Group 3) | 3737 - 94/3/1 (Group 3) | 3817 - 96/3/1 (Group 3) |
| Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. | One of mine. |
 |
 |
 |
| 3977 - 100/3/1 (Group3) | 4337 - 109/3/1 (Group 3) | 4977 - 125/3/1 (Group3) |
| One of mine. | Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. |
 |
 |
 |
| 21457 - 537/3/1 (Group 3) | 32137 - 804/3/1 (Group 3) | 39857 - 997/3/1 (Group 3) |
| One of mine. | One of mine. | Courtesy of Mark Gibson. |
 |
 |
 |
| 3418 - 86/3/2 (Group 3) | 4218 - 106/3/2 (Group 3) | 36658 - 917/3/2 (Group 3) |
| Courtesy of Steve Lawrie. | Courtesy of Andrew Ridley. | Courtesy of ibredguy.co.uk. |
 |
 |
 |
| 1699 - 43/3/3 (Group 3) | 1899 - 48/3/3 (Group 3) | 8019 - 201/3/3 (Group 3) |
| Courtesy of Mark Gibson. | Courtesy John A. McCulloch, © 2010 ARR. | One of mine. | Anonymous. |
 |
 |
 |
 |
| 13779 - 345/3/3 (Group 3) | 37899 - 948/3/3 (Group 3) | 500 - 13/3/4 (Group 3) | 2140 - 54/3/4 (Group 3) |
| One of mine. | One of mine. | Courtesy of mirak5 on ebay. |
 |
 |
 |
| 461 - 12/3/5 (Group 2) | 501 - 13/3/5 (Group 2) | 3141 - 79/3/5 (Group 2) |
| One of mine. | Courtesy of Mark Gibson. |
 |
 |
| 4501 - 113/3/5 (Group 2) | 9141 - 229/3/5 (Group 2) |
| Anonymous. | Courtesy of Steve Lawrie. | One of mine. |
 |
 |
 |
| 2102 - 53/3/6 (Group 2) | 3942 - 99/3/6 (Group 2) | 4502 - 113/3/6 (Group 2) |
| Courtesy of Steve Lawrie. | Courtesy of Mark Gibson. | Courtesy of Mark Gibson. | One of mine. |
 |
 |
 |
 |
| 13422 - 336/3/6 (Group 2) | 15102 - 378/3/6 (Group 2) | 1663 - 42/3/7 (Group 2) | 4503 - 113/3/7 (Group 2) |
| One of mine. | One of mine. | One of mine. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 4583 - 115/3/7 (Group 2) | 37903 - 948/3/7 (Group 2) | 424 - 11/3/8 (Group 2) | 2984 - 75/3/8 (Group 2) With imperf edge. |
| One of mine. | Courtesy of Steve Lawrie. | One of mine. | Courtesy of ibredguy.co.uk. |
 |
 |
 |
 |
| 4504 - 113/3/8 (Group 2) | 4864 - 122/3/8 (Group 2) | 4944 - 124/3/8 (Group 2) | 37904 - 948/3/8 (Group 2) |
Control 2984 above is the only one of these I have seen without perforations down the side. The 'MB-block' is perforated.
Was this an error, or was this done for a reason ?
| Row-4 PRIMARY flaws |
| Courtesy of Martien Blank. | Anonymous. | SECONDARY flaws | |
 |
 |
These have the following flaws in common:
Row-4, Stamp 1 Controls: 3785, 3825 small 16425 Using my 'widget' at the bottom gives me: 3785 = 95/4/1 3825 = 96/4/1 16425 = 411/4/1 16425 is part of the MB-block |
|
| 16425 | 3785 | ||
| Courtesy of the late Mike Holt. | Courtesy of Martien Blank. | SECONDARY flaws | |
 |
 |
These have the following features in common:
Row-4, Stamp 2 Controls: 3146, 3946 small 15106, 16426 Using my 'widget' at the bottom gives me: 3146 = 79/4/2 3946 = 99/4/2 15106 = 378/4/2 16426 = 411/4/2 16426 is from the MB-block. It shows no sign of the mark above 'MP' seen on the other two. |
|
| 3146 | 16426 | ||
| Courtesy of Martien Blank. | Courtesy of Steve Lawrie. | SECONDARY flaws | |
 |
 |
These have the following flaws in common:
Row-4, Stamp 3 Controls: 4147 small 8267, 16427, 37827 Using my 'widget' at the bottom gives me: 4147 = 104/4/3 8267 = 207/4/3 16427 = 411/4/3 37827 = 946/4/3 4147 adjoins 4148 below. 16427 is from the MB-block. |
|
| 16427 (small) | 37827 (small) | ||
| Courtesy of the late Mike Holt. | Courtesy of Martien Blank. | SECONDARY flaws | |
 |
 |
These have the following flaws in common:
Row-4, Stamp 4 Controls: 508, 2948, 4148, 8148 small 15108, 16428, 22748 Using my 'widget' at the bottom gives me: 508 = 13/4/4 2948 = 74/4/4 4148 = 104/4/4 8148 = 204/4/4 15108 = 378/4/4 16428 = 411/4/4 22748 = 569/4/4 Note on 508 a mark can be seen between frame-lines on the stamp below at Row-5, stamp 4. 16428 is part of the MB-block. 4148 adjoins 4147 above. |
|
| 508 | 16428 |
| One of mine. | Courtesy of Steve Lawrie. | SECONDARY flaws | |
 |
 |
These have the following features:
Row-4, Stamp 5 Controls: 2869, 3949 small: 9149, 15109 Using my 'widget' at the bottom gives me: 2869 = 72/4/5 3949 = 99/4/5 9149 = 229/4/5 15109 = 378/4/5 |
|
| 9149 | 3949 | ||
| Two of mine. | SECONDARY flaws | ||
 |
 |
This has the following flaws in common with 2/6.
Row-4, Stamp 6 Controls: 1190, 2150 Using my 'widget' at the bottom gives me: 1190 = 30/4/6 2150 = 54/4/6 These have an additional dot before 'D' of 'DISTRICT'. |
|
| 1190 | 2150 | ||
| Courtesy of Steve Lawrie. | Courtesy of ibredguy.co.uk. | SECONDARY flaws | |
 |
 |
Characteristic features:
Row-4, Stamp 7 Controls: 2111, 2831, 4991 small: 30231 Using my 'widget' at the bottom gives me: 2111 = 53/4/7 2831 = 71/4/7 4991 = 125/4/7 30231 = 756/4/7 |
|
| 30231 756/4/7 | 4991 125/4/7 | ||
| One of mine. | Courtesy of Les Bottomley | SECONDARY flaws | |
 |
 |
These have similarities with 2/8 and the following additional flaws:
Row-4, Stamp 8 Controls: 472, 3272, 3432, 3632 small: 4872, 16032 Using my 'widget' at the bottom gives me: 472 = 12/4/8 3272 = 82/4/8 3432 = 86/4/8 3632 = 91/4/8 4872 = 122/4/8 16032 = 401/4/8 Some of the flaws look rather weak on 472, 4872 and 16032. |
|
| 3632 | 16032 |
| Anonymous. | Courtesy of Andrew Higson. | Courtesy of Martien Blank. |
 |
 |
 |
| 3785 - 95/4/1 (Group 4) | 3825 - 96/4/1 (Group 4) | 16425 - 411/4/1 (Group 4) |
| Courtesy of Steve Lawrie. | Courtesy of Andrew Higson. | One of mine. | Courtesy of Martien Blank. |
 |
 |
 |
 |
| 3146 - 79/4/2 (Group 4) | 3946 - 99/4/2 (Group 4) | 15106 - 378/4/2 (Group 4) | 16426 - 411/4/2 (Group 4) |
| Courtesy of Steve Lawrie. | Courtesy of the late Mike Holt. | Courtesy of Martien Blank. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 4147 - 104/4/3 (Group 4) | 8267 - 207/4/3 (Group 4) | 16427 - 411/4/3 (Group 4) | 37827 - 946/4/3 (Group 4) |
| Courtesy of the late Mike Holt. | Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. | Courtesy of Mark Gibson. |
 |
 |
 |
 |
| 508 - 13/4/4 (Group 4) | 2948 - 74/4/4 (Group 4) | 4148 - 104/4/4 (Group 4) | 8148 - 204/4/4 (Group 4) |
| Courtesy Spink and Son. | Courtesy of Martien Blank. | Courtesy of Steve Lawrie. |
 |
 |
 |
| 15108 - 378/4/4 (Group 4) | 16428 - 411/4/4 (Group 4) | 22748 - 569/4/4 (Group 4) |
| Courtesy of Mark Gibson. | Courtesy of Steve Lawrie | One of mine. | One of mine. |
 |
 |
 |
 |
| 2869 - 72/4/5 (Group 1) | 3949 - 99/4/5 (Group 1) | 9149 - 229/4/5 (Group 1) | 15109 - 378/4/5 (Group 1) |
| One of mine. | One of mine. |
 |
 |
| 1190 - 30/4/6 (Group 1) | 2150 - 54/4/6 (Group 1) |
| One of mine. | Courtesy of ibredguy.co.uk. | Courtesy of ibredguy.co.uk. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 2111 - 53/4/7 (Group 1) | 2831 - 71/4/7 (Group 1) | 4991 - 125/4/7 (Group 1) | 30231 - 756/4/7 (Group 1) |
| One of mine. | Courtesy of Mark Gibson. | Courtesy of Steve Lawrie. |
 |
 |
 |
| 472 - 12/4/8 (Group 1) | 3272 - 82/4/8 (Group 1) | 3432 - 86/4/8 (Group 1) |
| One of mine. | Courtesy of Stephen Gardner. | Courtesy of Les Bottomley. |
 |
 |
 |
| 3632 - 91/4/8 (Group 1) | 4872 - 122/4/8 (Group 1) | 16032 - 401/4/8 (Group 1) |
| Row-5 PRIMARY flaws These are all from Group 5
|
| Courtesy of Martien Blank. | Courtesy of Mark Gibson. | SECONDARY flaws | |
 |
 |
These have the following flaws in common:
Row-5, Stamp 1 Controls: 833, 1713, 1913, 2993, 5433 small 16433, 27553, 36673 Using my 'widget' at the bottom gives me: 833 = 21/5/1 1713 = 43/5/1 1913 = 48/5/1 2993 = 75/5/1 5433 = 136/5/1 16433 = 411/5/1 27553 = 689/5/1 36673 = 917/5/1 16433 is part of the MB-block.. |
|
| 1713 | 27553 (small) | ||
| Courtesy of Martien Blank. | One of mine. | SECONDARY flaws | |
 |
 |
These have the following distinctive flaws:
Row-5, Stamp 2 Controls: 514, 1714, 2834 small 1954, 16434, 19234, 31114 Using my 'widget' at the bottom gives me: 514 = 13/5/2 1714 = 43/5/2 1954 = 49/5/2 2834 = 71/5/2 16434 = 411/5/2 19234 = 481/5/2 31114 =778/5/2 1714 adjoins 1713 above. 19234 adjoins 19235 below. 16434 is from the MB-block. |
|
| 16434 (small) | 19234 (small) | ||
| One of mine. | Courtesy of Martien Blank. | SECONDARY flaws | |
 |
 |
This pair have the following flaws in common.
This is very similar to Row-5, Stamp 7. |
|
| 4955 | 16435 | ||
| Courtesy of Martien Blank. | Anonymous. | SECONDARY flaws | |
 |
 |
These have the following flaws in common:
Row-5, Stamp 4 Controls: 2836, 4036, 4116, 4436 small 16436 Using my 'widget' at the bottom gives me: 2836 = 71/5/4 4036 = 101/5/4 4116 = 103/5/4 4436 = 111/5/4 16436 = 411/5/4 Note, the mark at the top can be seen on one of the Row-4/4 stamps above. 16436 is part of the MB-block. |
|
| 16436 | 4436 | ||
| Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. | SECONDARY flaws | |
 |
 |
These have the following distinctive features:
|
|
| 477 | 1037 (small) | ||
| One of mine. | Courtesy of Steve Lawrie. | SECONDARY flaws | |
 |
 |
These have the following distinctive features:
|
|
| 918 | 2838 | ||
| One of mine. | Courtesy of Martien Blank. | SECONDARY flaws | |
 |
 |
These have the following flaws in common.
Row-5, Stamp 7 Controls: 559, 1199, 2119, 3319 small: 8239, 16839 Using my 'widget' at the bottom gives me: 559 = 14/5/7 1199 = 30/5/7 2119 = 53/5/7 3319 = 83/5/7 8239 = 206/5/7 16839 = 421/5/7 This is very similar to Row-5 stamp 3 559 adjoins 560 below. |
|
| 3319 | 16839 | ||
| Courtesy of Mark Gibson. | Courtesy of Mark Gibson. | SECONDARY flaws | |
 |
 |
These have the following flaws in common:
Row-5, Stamp 8 Controls: 560, 1200, 2840, 3160, 4960, 8600 Using my 'widget' at the bottom gives me: 560 = 14/5/8) 1200 = 30/5/8 2840 =71/5/8) 3160 =79/5/8) 4960 = 124/5/8 8600 =215/5/8) 560 adjoins 559 above. 4960 is close to 4955 above. |
|
| 560 | 8600 |
| Courtesy of Steve Lawrie. | Anonymous. | Reproduced with permission from http://www.stampboards.com | Anonymous. |
 |
 |
 |
 |
| 833 - 21/5/1 (Group 5) | 1713 - 43/5/1 (Group 5) | 1913 - 48/5/1 (Group 5) | 2993 - 75/5/1 (Group 5) |
| One of mine. | Courtesy of Martien Blank. | Courtesy of Mark Gibson. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 5433 - 136/5/1 (Group 5) | 16433 - 411/5/1 (Group 5) | 27553 - 689/5/1 (Group 5) | 36673 - 917/5/1 (Group 5) |
| One of mine | Anonymous. | Courtesy of Steve Lawrie. | Courtesy of ibredguy.co.uk. |
 |
 |
 |
 |
| 514 - 13/5/2 (Group 5) | 1714 - 43/5/2 (Group 5) | 1954 - 48/5/2 (Group 5) | 2834 - 71/5/2 (Group 5) |
| Courtesy of Martien Blank. | One of mine. | Courtesy of Mark Talbot. |
 |
 |
 |
| 16434 - 411/5/2 (Group 5) | 19234 - 481/5/2 (Group 5) | 31114 - 778/5/2 (Group 5) |
| One of mine. | Courtesy of Martien Blank. | Courtesy of Mike Jackson. |
 |
 |
 |
| 4955 - 124/5/3 (Group 5) | 16435 - 411/5/3 (Group 5) | 19235 - 481/5/3 (Group 5) |
| One of mine. | Courtesy of the late Mike Holt. | Anonymous. | Anonymous. |
 |
 |
 |
 |
| 2836 - 71/5/4 (Group 5) | 4036 - 101/5/4 (Group 5) | 4116 - 103/5/4 (Group 5) | 4436 - 111/5/4 (Group 5) |
| Courtesy of Martien Blank. | Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 16436 - 411/5/4 (Group 5) | 477 - 12/5/5 (Group 5) | 1037 - 26/5/5 (Group 5) | 4517 - 113/5/5 (Group 5) |
| One of mine. | Courtesy of Steve Lawrie. | One of mine. | Courtesy of Steve Lawrie. |
 |
 |
 |
 |
| 918 - 23/5/6 (Group 5) | 2838 - 71/5/6 (Group 5) | 3158 - 79/5/6 (Group 5) | 3878 - 97/5/6 (Group 5) |
| Anonymous. | Courtesy of Mark Gibson. | One of mine. |
 |
 |
 |
| 15118 - 378/5/6 (Group 5) | 559 - 14/5/7 (Group 5) | 1199 - 30/5/7 (Group 5) |
| Courtesy of Steve Lawrie. | One of mine. | Courtesy of Steve Lawrie. | One of mine. |
 |
 |
 |
 |
| 2119 - 53/5/7 (Group 5) | 3319 - 83/5/7 (Group 5) | 8239 - 206/5/7 (Group 5) | 16839 - 421/5/7 (Group 5) |
| Courtesy of Mark Gibson. | Courtesy of ibredguy.co.uk. | Courtesy of Mark Talbot. |
 |
 |
 |
| 560 - 14/5/8 (Group 5) | 1200 - 30/5/8 (Group 5) | 2840 - 71/5/8 (Group 5) |
| One of mine. | Anonymous. | Courtesy of Mark Gibson. |
 |
 |
 |
| 3160 - 79/5/8 (Group 5) | 4960 - 124/5/8 (Group 5) | 8600 - 215/5/8 (Group 5) |
Here is an interesting series:
 |
 |
 |
 |
| 1557 (large - 39/5/5) | 1569 (small - 40/2/1) | 1576 (large - 40/2/8) | 1589 (small - 40/4/5) |
I think it unlikely that it is the same 'sheet 40' for both large and small controls.
I think it is possible that the same number may exist with large and small controls.
There are several possibilities, either large and small were used concurrently from the beginning, and the large either discarded (or not) when it got to maximum count.
Alternatively The large could have been used first and replaced by the small when it got to the maximum count (or before).
I do not see the small being used first, then replaced by the large (having less digits) unless of course it had more digits that never got used.
However the highest count I have seen is less than 40,000 and I'm sure we would have seen numbers above that if they all came before the large controls.
Look closely at the pair below. It may provide the answer.
 |
| 1105 (28/4/1) fairly well centred, and 1106 (28/4/2) poorly centred. I would have expected this (digitally constructed) pair to fit together better if they were from the same sheet. However, most of my reconstructions are compatible, so I suspect that the re-use was only until a replacement machine with more digits could be obtained. Alternatively, all the used examples are from a narrow time period (the takeover) and previous ones were destroyed. It should also be noted though that as well as the 4879/4880 pair shown, I have seen 4886 and 4893, but nothing higher than these, another indication of a narrow time slice. |
| 3d | Column Number | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 1 | 1/1 (1481) |
1/2 (3 stamps) |
1/3 (4 stamps) |
1/4 (4 stamps) |
1/5 (7 stamps) |
1/6 (5 stamps) |
1/7 (6 stamps) |
1/8 (3 stamps) |
||
| 2 | 2/1 (5 stamps) |
2/2 (5 stamps) |
2/3 (4 stamps) |
2/4 (9 stamps) | 2/5 (7 stamps) |
2/6 (4 stamps) |
2/7 (3 stamps) |
2/8 (9 stamps) |
||
| 3 | 3/1 (2 stamps) |
3/2 (2 stamps) |
3/3 (8 stamps) |
3/4 (6 stamps) | 3/5 (2 stamps) |
3/6 (8 stamps) |
3/7 (2743) |
3/8 (2 stamps) |
||
| 4 | 4/1 (12 stamps) |
4/2 (6 stamps) |
4/3 (3 stamps) |
4/4 (4 stamps) |
4/5 (4 stamps) |
4/6 (2 stamps) |
4/7 (5 stamps) |
4/8 (3 stamps) |
||
| 5 | 5/1 (3 stamps) |
5/2 (3 stamps) |
5/3 (5 stamps) |
5/4 (3 stamps) | 5/5 (5 stamps) |
5/6 (4 stamps) |
5/7 (6 stamps) |
5/8 (6 stamps) |
||
When I started to classify the flaws into groups, I had in mind that each group would represent a member of the transfer group.
On the Waterlow sheets the transfer group was a half-row of stamps.
Here it was a column of 5 stamps which was used to create half of the columns. This was copied by transfer to create the other half of the plate.
I think columns 1 to 4 were created first and 5 to 8 were the copies since 2/5 has an extra mark not present on 2/1.
The 6d was not done the same way.
| 6d | Column Number | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 1 | Group 4 (6 stamps) |
Group 4 (3 stamps) |
Group 4 (5 stamps) |
Group 4 (3 stamps) | Group 3 (4 stamps) |
Group 3 (4 stamps) |
Group 3 (4 stamps) |
Group 3 (2 stamps) |
||
| 2 | Group 2 (4 stamps) |
Group 2 (2 stamps) |
Group 2 (5 stamps) |
Group 2 (7 stamps) |
Group 1 (8 stamps) |
Group 1 (1694) |
Group 1 (8 stamps) |
Group 1 (6 stamps) |
||
| 3 | Group 3 (9 stamps) |
Group 3 (3 stamps) |
Group 3 (5 stamps) |
Group 3 (2 stamps) |
Group 2 (5 stamps) |
Group 2 (5 stamps) |
Group 2 (4 stamps) |
Group 2 (6 stamps) |
||
| 4 | Group 4 (3 stamps) |
Group 4 (4 stamps) |
Group 4 (4 stamps) |
Group 4 (7 stamps) |
Group 1 (4 stamps) |
Group 1 (2 stamps) |
Group 1 (4 stamps) |
Group 1 (6 stamps) |
||
| 5 | Group 5 (8 stamps) |
Group 5 (7 stamps) |
Group 5 (3 stamps) |
Group 5 (5 stamps) |
Group 5 (3 stamps) |
Group 5 (5 stamps) |
Group 5 (6 stamps) |
Group 5 (6 stamps) |
||
The 3d stamps were easier to plate, with those, most of the discrepancies resulted from a 4-column difference.
It suggests that in each row, the second batch of 4 stamps are a repeat of the first batch with minor (usually) differences.
I now get a 100% reconstruction this way.
The 6d are more complicated, causing me to think they were not all stamps from sheets having 5 rows of 8.
I tried to match the remainder with booklets of 2 rows of 6, or 10 rows of 12, but neither worked.
Now, by accepting that four of the positions have some minor differences, I have 100% reconstruction.
The differences are mostly between the large and small controls, and suggest cleaning of the plate at some stage.
The difference between groups on the left hand and right hand halves of the 6d also made
me wonder if there were in fact two plates, each having 5 rows of 4 stamps each. I wanted a pair that straddled column 4 and 5.
Multiples, even joined halves are scarce, but I can show a pair that was once joined:

This shows fairly convincingly that these were once joined as Sheet 83, row 2, stamps 4 and 5.
Stamp 4 being from Group-2, and stamp 5 from Group-1.
* Assuming the highest control number seen reflects the quantity issued.
These figures beg an explanation.
The survival rate for Large controls is higher for used stamps, whereas for Small controls it is higher for unused.
Fortunately there may be an explanation.
Steven Roberts records about halfway down
Competitors Allies, the Companies' claim:
“The low rate charged for messages, sixpence for fifteen words exclusive of address, and half-rates for pre-paid answers,
does not by any means affect the precautions taken for the safe keeping and delivery of the messages entrusted to the Company’s care.
Each receives its particular and goes through its regular course from desk to desk and room to room, until its work is finally accomplished,
when it is carefully put up in company with all papers bearing in any way upon it, and preserved for three months
in one of the numerous presses close at hand, from thence to descend at the end of that period to the cellar,
after a two years’ sojourn in which it is finally destroyed.”
The used LDTC stamps currently available can then be seen as (primarily) a sample of
the last two years or so of the companies telegraph forms, 'liberated' at the time of its' takeover.
These would seem to be mostly Large controls! This is a great surprise to me, but (at the moment) I can see no other interpretation.
It might also explain why there are so many unused small control stamps about if they were left over at the end.
My chief objection to this is that mainly the 6d were used and if they only used 8600 of these in 2 years, that implies about 12 per day !
Not exactly the usage I would expect for the whole of London.
This suggests that the majority were diligently destroyed at the takeover, or perhaps handed over to the Post Office.
Perhaps a member of Post office staff was responsible for releasing most of the existing ones.
The control-number sequence can be used over and over, but pairs tend to mostly match-up and I would expect to see some in the 9000's.
 |
 |
| Courtesy of Martien Blank. | Courtesy of the late Mike Holt. (Now also owned by Martien Blank). |
| Two examples of 3d, large control 4216 (row 2, column 8). Used and unused. Clearly the numbers were re-used. An adjoining stamp is only likely to match one of them. |
|
Possibly each branch was sent a batch of sheets and used them sequentially, with the used examples coming from only one or two branches.
Unused examples would be a combination of those deliberately 'collected' plus leftovers after the Post Office takeover.
The most telling piece of evidence is the fact that most of the cancelled large control stamps still have their gum.
This implies that they were pre-cancelled ready for use, but not in fact used.
Almost certainly this is because the Post Office takeover intervened, which would imply that these were the type last used.
Last updated 1st. January 2026
©Copyright Steve Panting 2012/13/14/15/16/17/18/19/20/21/22/23/24/25/26 except where stated.
Permission is hereby granted to copy material for which the copyright is owned by myself, on condition that any data is not altered and this website is given credit.